Image Details
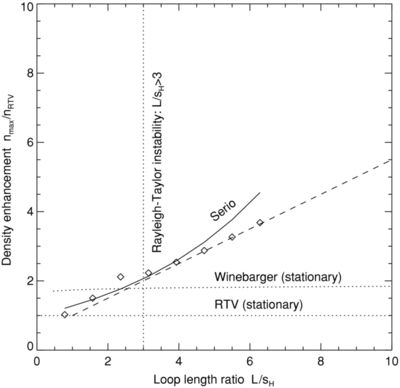
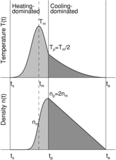
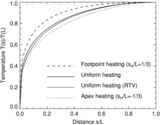
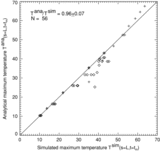
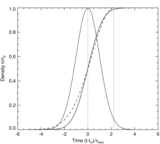
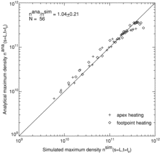
Caption: Figure 5.
Maximum density enhancement with respect to the RTV density,
n
p
/
n
RTV as a function of the ratio of loop half-length to heating scale height,
L/
s
H
, for a set of eight hydrodynamic numerical simulations performed by Tsiklauri et al. (2004), for
s
H
= 8.75 Mm and loop half-lengths of
L = 9, ..., 55 Mm (diamonds). The scaling law of Serio et al. (1981) yields consistent predictions for
L/
s
H
![]() 3, but overpredicts the density enhancements for higher values of
L/
s
H
3, but overpredicts the density enhancements for higher values of
L/
s
H
![]() 3 where no stationary loop solutions exist due to the Rayleigh–Taylor instability. Numerical hydrodynamic simulations yield
maximum density enhancements of
n
p
/
n
RTV ≲ 2 for stationary solutions (Winebarger et al. 2003a, 2003b). For dynamic simulations of impulsive heating and subsequent
cooling maximum (Tsiklauri et al. 2004), maximum density enhancements of
n
max/
n
RTV ≈ 0.5(1 +
L/
s
H
) are obtained.
3 where no stationary loop solutions exist due to the Rayleigh–Taylor instability. Numerical hydrodynamic simulations yield
maximum density enhancements of
n
p
/
n
RTV ≲ 2 for stationary solutions (Winebarger et al. 2003a, 2003b). For dynamic simulations of impulsive heating and subsequent
cooling maximum (Tsiklauri et al. 2004), maximum density enhancements of
n
max/
n
RTV ≈ 0.5(1 +
L/
s
H
) are obtained.
Copyright and Terms & Conditions
© 2009. The American Astronomical Society. All rights reserved.