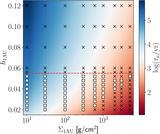
Image Details
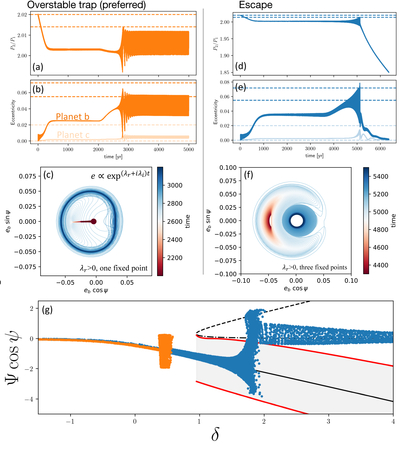
Caption: Figure 9.
Outcomes of the dissipative resonant evolution of TOI-4495 analogs, categorized by the stability of equilibrium points and the number of fixed points at capture. Panels (a)–(c): period ratio, eccentricity, and resonant angle ψ during an overstable trap. In this regime, the real part of the eigenvalue is positive (λr > 0), but the resonant fixed point has not bifurcated. Eccentricities are excited and saturate at finite values, leading to wide oscillations around the equilibrium. Panels (d)–(f): the same quantities for resonant escape. Here, the real part of the eigenvalue is positive, and the conservative fixed point has bifurcated. Eccentricities continue to grow until the system crosses into the inner circulation region, moving narrowly away from the 2:1 MMR. The planets then escape resonance and migrate toward more compact commensurabilities. The dashed lines in the first two columns mark the observed period ratios and eccentricities of TOI-4495. Panel (g): phase-space evolution of the two cases. Both satisfy the analytic overstable condition (λr > 0). In the trap case, the system reaches equilibrium before bifurcation (δ < 0.95), while in the escape case, the trajectory evolves beyond bifurcation (δ > 0.95), resulting in resonant departure.
Copyright and Terms & Conditions
© 2026. The Author(s). Published by the American Astronomical Society.