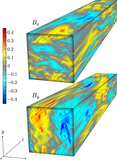
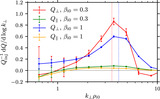
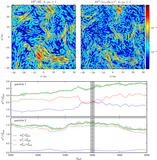
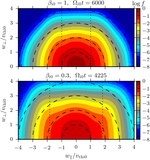
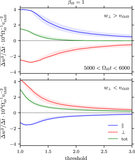
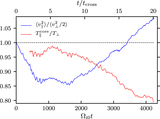
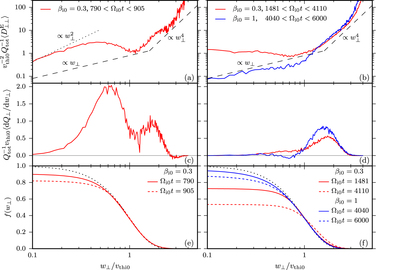
Box-averaged perpendicular-energy diffusion coefficient, ﹩\langle {D}_{\perp \perp }^{{\rm{E}}}\rangle ﹩ (see Equation (10)), averaged over two time windows: (a) at early times, during which the core of the perpendicular distribution function becomes appreciably flattened, and (b) at late times after f(w_⊥) is cored and during which its temperature steadily grows (the stated values of ﹩{T}_{\perp }^{\mathrm{tail}}/{T}_{{\rm{i}}0}﹩ are obtained from a Maxwellian fit to the ﹩{w}_{\perp }/{v}_{\mathrm{thi}0}\gt 1﹩ tail of the distribution function). At late times, the diffusion coefficient is flat for ﹩{w}_{\perp }\lt {v}_{\mathrm{thi}0};﹩ because df(w_⊥)/dw_⊥ ∼ 0 in this range, very little heating happens at small velocities. At larger velocities, ﹩\langle {D}_{\perp \perp }^{{\rm{E}}}\rangle \propto {w}_{\,\perp }^{4}﹩ seems to be a fair approximation. In all panels, “⊥” is measured with respect to the magnetic field at the location of each particle.