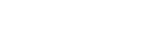Image Details
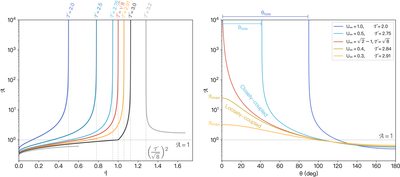
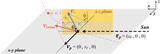
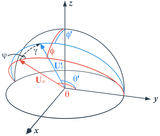
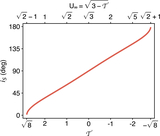
Caption: Figure 2.
Left: constant ﹩{ \mathcal T }﹩ curves on the dimensionless ﹩{\unicode{120006}}﹩–﹩{ \mathcal A }﹩ (perihelion distance–semimajor axis) space, assuming i = 0° (Equation (10)). In the large-﹩{ \mathcal A }﹩ limit, ﹩{\unicode{120006}}﹩ asymptotically approaches the value ﹩{({ \mathcal T }/\sqrt{8})}^{2}﹩ (vertical gray dashed lines, Equation (11). For ﹩{ \mathcal T }\lt \sqrt{8}﹩, ﹩{{\rm{lim}}}_{{ \mathcal A }\to \infty }{\unicode{120006}}\lt 1﹩ and the particle can never decouple from the planet in the coplanar case (blue). For ﹩{ \mathcal T }\gt \sqrt{8}﹩, ﹩{{\rm{lim}}}_{{ \mathcal A }\to \infty }{\unicode{120006}}\gt 1﹩ and spontaneous decoupling when the particle reaches large ﹩{ \mathcal A }﹩ is guaranteed (orange). The loosely coupled case and the closely coupled cases defined in text are separated by the critical value of ﹩{ \mathcal T }=\sqrt{8}﹩ (red), which has ﹩{\unicode{120006}}﹩ → 1 as ﹩{ \mathcal A }\to \infty ﹩. Equation (10) is partially undefined near the planet for ﹩{ \mathcal T }\gt 3﹩ (gray). Right: ﹩{ \mathcal A }﹩ as a function of θ for various U∞ (Equation (5)). The horizontal dashed line marks ﹩{ \mathcal A }=1﹩. In a loosely coupled case (golden curves), there is a maximum ﹩{ \mathcal A }﹩ that the particle can reach in the planet-crossing state. For the boundary case ﹩{U}_{\infty }=\sqrt{2}-1﹩ (orange), θ → 0° corresponds to ﹩{ \mathcal A }\to \infty ﹩. In closely coupled cases (blue), the object will escape the system once θ < θloss, which is defined in Equation (13). A larger U∞ corresponds to a wider loss cone (blue line segments).
Copyright and Terms & Conditions
© 2026. The Author(s). Published by the American Astronomical Society.