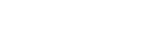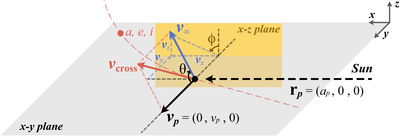
Schematic illustration of the 3D scattering geometry in a planet-centered corotating frame. The z-axis (﹩\hat{{\boldsymbol{k}}}﹩) points out of the orbital plane, while the x-axis (﹩\hat{{\boldsymbol{i}}}﹩) and y-axis (﹩\hat{{\boldsymbol{j}}}﹩) are aligned respectively with the instantaneous radial and transverse directions of the planet at the time of encounter. In this coordinate system, r_p lies entirely along the x-axis, and v_p (the planet’s velocity, solid black arrow) lies along the y-axis. The small-body’s heliocentric velocity vector at the intersection v_cross (solid red arrow) is the vector sum of the relative-velocity vector v_∞ (solid blue arrow) and v_p. The vector U_∞ = v_∞/v_p is the normalized relative velocity. The two angles θ (the polar angle from v_p) and ϕ (the azimuth angle of v_∞ in the x–z plane) fully specify the direction of the relative-velocity vector.