Image Details
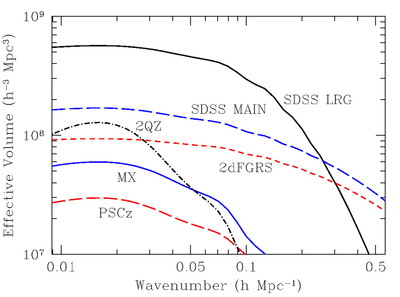
Caption: Fig. 1.
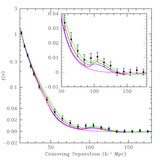
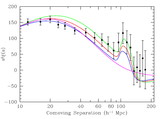
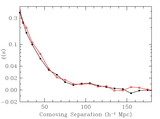
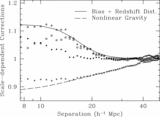
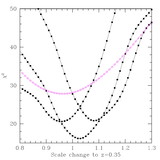
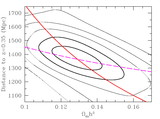
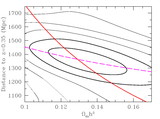
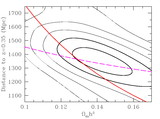
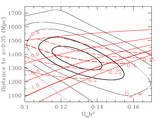
Effective volume (eq. [1]) as a function of wavenumber for various large redshift surveys. The effective volume is a rough guide to the performance of a survey (errors scaling as ﹩V^{-1/ 2}_{\mathrm{eff}\,}﹩) but should not be trusted to better than 30%. To facilitate comparison, we have assumed 3816 deg2 for the SDSS main sample, the same area as the SDSS LRG sample presented in this paper and similar to the area in Data Release 3. This is about 50% larger than the sample analyzed in Tegmark et al. (2004a), which would be similar to the curve for the full 2dFGRS (Colless et al. 2003). We have neglected the potential gains on very large scales from the 99 outrigger fields of the 2dFGRS. The other surveys are the MX survey of clusters (Miller & Batuski 2001), the PSCz survey of galaxies (Sutherland et al. 1999), and the 2QZ survey of quasars (Croom et al. 2004). The SDSS DR3 quasar survey (Schneider et al. 2005) is similar in effective volume to the 2QZ. For the amplitude of P(k), we have used ﹩\sigma _{8}=1﹩ for 2QZ and PSCz and 3.6 for the MX survey. We used ﹩\sigma _{8}=1.8﹩ for SDSS LRG, SDSS main, and the 2dFGRS. For the latter two, this value represents the amplitude of clustering of the luminous galaxies at the surveys’ edge; at lower redshift, the number density is so high that the choice of σ8 is irrelevant. Reducing SDSS main or 2dFGRS to ﹩\sigma _{8}=1﹩, the value typical of normal galaxies, decreases their Veff by 30%.
Copyright and Terms & Conditions
© 2005. The American Astronomical Society. All rights reserved. Printed in U.S.A.