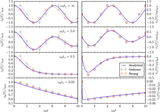
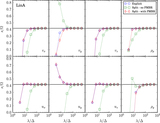
Image Details
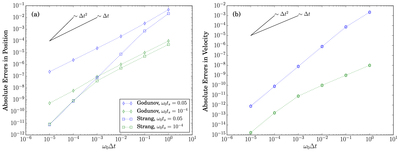
Caption: Figure 3.
Absolute errors in (a) position and (b) velocity as a function of time step ﹩{\rm{\Delta }}t﹩ for two over-damped harmonic oscillators. The position is normalized by the initial position ﹩{z}_{p,0}﹩, while the velocity is normalized by ﹩{\omega }_{0}{z}_{p,0}﹩, where ﹩{\omega }_{0}﹩ is the natural frequency of the oscillator. The errors are measured at a fixed final time of ﹩t={\omega }_{0}^{-1}﹩. The diamond and the square symbols are the results using the Godunov and the Strang splitting methods, respectively. The blue and the green colors denote a stopping time of ﹩{t}_{s}=0.05{\omega }_{0}^{-1}﹩ and ﹩{t}_{s}={10}^{-4}{\omega }_{0}^{-1}﹩, respectively. The solid lines guide the slopes for first- or second-order convergence.
Copyright and Terms & Conditions
© 2016. The American Astronomical Society. All rights reserved.