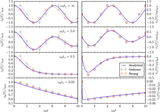
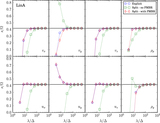
Image Details
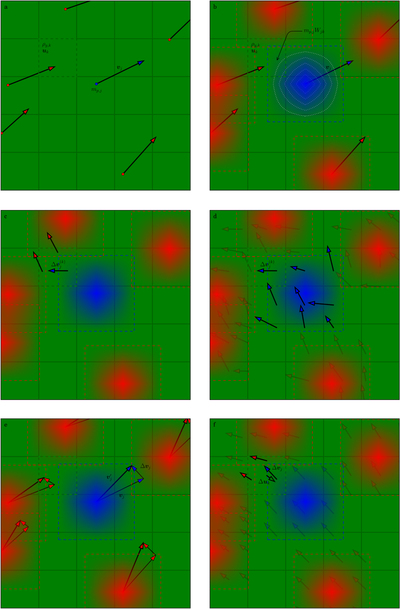
Caption: Figure 1.
Schematic diagrams in two dimensions, demonstrating the particle-mesh scheme we use to integrate the mutual drag force. (a) A grid of gas cells with several Lagrangian solid particles. The jth particle (shown in blue) has a mass of ﹩{m}_{p,j}﹩ and a velocity of ﹩{{\boldsymbol{v}}}_{j}﹩. The green dashed line shows the boundary of cell k, in which the gas has a density of ﹩{\rho }_{g,k}﹩ and a velocity of ﹩{{\boldsymbol{u}}}_{k}﹩. (b) Each particle is interpreted as a distributed cloud, with its boundary shown by a blue or red dashed line. The white dotted lines are the density contours for the jth particle. Each particle cloud is further split by the grid cells into sub-clouds, each of which has the same initial velocity ﹩{{\boldsymbol{v}}}_{j}﹩ as the parent particle. The mass of the sub-cloud from the jth particle that is enclosed in cell k is ﹩{m}_{p,j}{W}_{{jk}}﹩, where ﹩{W}_{{jk}}\equiv W({{\boldsymbol{r}}}_{p,j}-{{\boldsymbol{r}}}_{k})﹩. (c) Within cell k, the enclosed sub-clouds are allowed to interact with the gas as well as each other via the mutual drag force, independent of the other sub-clouds in other cells. The sub-cloud from the jth particle thus receives a change in velocity ﹩{\rm{\Delta }}{{\boldsymbol{v}}}_{j}^{(k)}﹩ over a finite time step ﹩{\rm{\Delta }}t﹩, similarly for the other sub-clouds in the same cell. (d) The same operation is applied to every cell, and thus all sub-clouds undergo a change in velocity. (e) The total change in velocity for the jth particle ﹩{\rm{\Delta }}{{\boldsymbol{v}}}_{j}﹩ is then the weighted summation of all ﹩{\rm{\Delta }}{{\boldsymbol{v}}}_{j}^{(k)}﹩'s of its sub-clouds. As a result, the velocity of the jth particle becomes ﹩{{\boldsymbol{v}}}_{j}^{\prime }﹩ at the next time step, similarly for all other particles. (f) To find the change in the velocity field of the gas, we once again apply the interpretation of the sub-particle clouds, except that each sub-cloud from the jth particle now has the same change of velocity ﹩{\rm{\Delta }}{{\boldsymbol{v}}}_{j}﹩ as its parent particle cloud. Because the change in total momentum for cell k is known, the change of gas velocity ﹩{\rm{\Delta }}{{\boldsymbol{u}}}_{k}﹩ in the cell can be computed from the momentum changes of the sub-particle clouds in the cell. We dub this last procedure “particle-mesh back reaction.”
Copyright and Terms & Conditions
© 2016. The American Astronomical Society. All rights reserved.