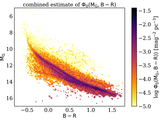
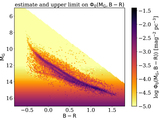
Image Details
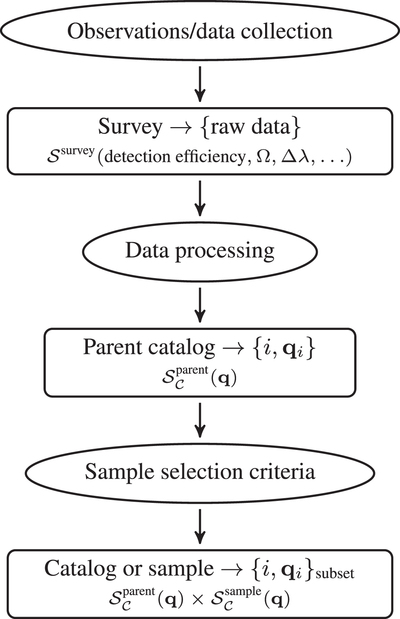
Caption: Figure 1.
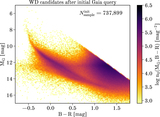
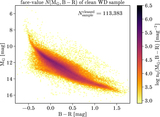
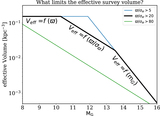
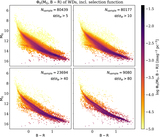
Schematic of all the factors that sequentially set the selection function ﹩{S}_{{ \mathcal C }}({\boldsymbol{q}})﹩ of a sample of discrete astrophysical objects to be modeled. ﹩{S}_{{ \mathcal C }}({\boldsymbol{q}})﹩ describes the probability that such an object with observable properties q will enter a sample. Viewed end to end, this starts with the overall experiment (say, the Gaia mission) and its detection efficiency of astrophysical sources, Ssurvey. After data processing, this results in a parent catalog (say, the Gaia EDR3 catalog), whose completeness, ﹩{S}_{{ \mathcal C }}^{\mathrm{parent}}({\boldsymbol{q}})﹩, must be characterized. Astrophysical models for some class of objects can then be constrained by comparison with catalog data. But in practice, only a (often tiny) subset of objects in the entire parent catalog will be modeled. Commonly, these are objects that represent some particular class of astrophysical objects, say, white dwarfs, or QSO, etc. Such subsamples are typically defined through a set of selection “cuts,” ﹩{S}_{{ \mathcal C }}^{\mathrm{sample}}({\boldsymbol{q}})﹩. In the end, the individual selection function factors are multiplied and summarized in the overall selection function, ﹩{S}_{{ \mathcal C }}({\boldsymbol{q}})﹩. In practice, the parent catalog completeness, ﹩{S}_{{ \mathcal C }}^{\mathrm{parent}}({\boldsymbol{q}})﹩ is often the same “given” across many modeling applications, while the sample selection ﹩{S}_{{ \mathcal C }}^{\mathrm{sample}}({\boldsymbol{q}})﹩ will always be tailored to the astrophysical case at hand.
Copyright and Terms & Conditions
© 2021. The Author(s). Published by the American Astronomical Society.