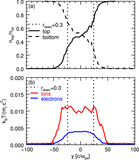
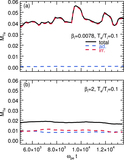
Image Details
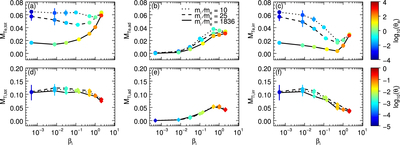
Caption: Figure 12.
Mass ratio ﹩{m}_{{\rm{i}}}/{m}_{{\rm{e}}}﹩ dependence of heating efficiencies: (a) electron total, ﹩{M}_{T{\rm{e}},\mathrm{tot}};﹩ (b) electron adiabatic, ﹩{M}_{T{\rm{e}},\mathrm{ad}};﹩ (c) electron irreversible, ﹩{M}_{T{\rm{e}},\mathrm{irr}};﹩ (d) proton total, ﹩{M}_{T{\rm{i}},\mathrm{tot}};﹩ (e) proton adiabatic, ﹩{M}_{T{\rm{i}},\mathrm{ad}};﹩ and (f) proton irreversible, ﹩{M}_{T{\rm{i}},\mathrm{irr}}﹩, for ﹩{T}_{{\rm{e}}}/{T}_{{\rm{i}}}=1﹩ simulations with mass ratios ﹩{m}_{{\rm{i}}}/{m}_{{\rm{e}}}=10﹩ (dotted), 25 (dashed), and 1836 (solid). The legend is located in the upper part of panel (b). Points in panels (a)–(c) are colored according to electron dimensionless temperature in the upstream (color bar is to the right of panel (c)), and points in panels (d)–(f) are colored according to proton dimensionless temperature in the upstream (color bar is to the right of panel (f)). The irreversible heating is remarkably independent of mass ratio at high ﹩{\beta }_{{\rm{i}}}(=2),﹩ while at low ﹩{\beta }_{{\rm{i}}}﹩, the irreversible electron heating efficiency decreases with increasing mass ratio.
Copyright and Terms & Conditions
© 2017. The American Astronomical Society. All rights reserved.