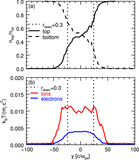
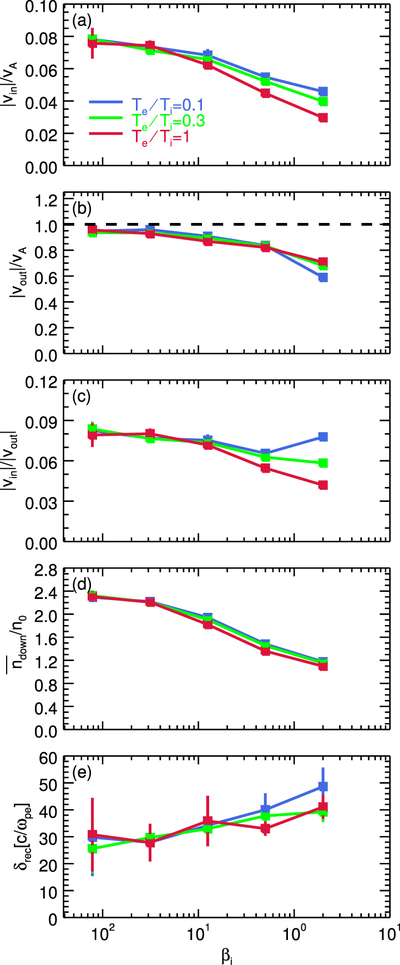
For temperature ratios ﹩{T}_{{\rm{e}}}/{T}_{{\rm{i}}}=0.1﹩ (blue), 0.3 (green), and 1 (red), ﹩{\beta }_{{\rm{i}}}﹩ dependence of (a) inflow velocity ﹩| {v}_{\mathrm{in}}| /{v}_{{\rm{A}}};﹩ (b) outflow velocity ﹩| {v}_{\mathrm{out}}| /{v}_{{\rm{A}}};﹩ (c) reconnection rate ﹩| {v}_{\mathrm{in}}| /| {v}_{\mathrm{out}}| ;﹩ (d) downstream density in units of initial density in the upstream ﹩{\overline{n}}_{\mathrm{down}}/{n}_{0};﹩ and (e) width of reconnection layer ﹩{\delta }_{\mathrm{rec}}﹩. Error bars represent one standard deviation from the mean. The inflow velocity is averaged over a region of length ﹩{L}_{x}/3\approx 1440c/{\omega }_{\mathrm{pe}}﹩ in x and width ﹩20\,c/{\omega }_{\mathrm{pe}}﹩ in y, located ﹩| y| \sim 100\,c/{\omega }_{\mathrm{pe}}﹩ upstream of the central X-point. We have checked that the saturation value is insensitive to the choice of averaging region. The outflow velocity is computed as an average over the 20 cells with the largest ﹩| {\boldsymbol{v}}\cdot \hat{{\boldsymbol{x}}}| ﹩ located along the central region of the outflow (﹩| y| \lesssim 4\,c/{\omega }_{\mathrm{pe}}﹩). We have tested that the resulting outflow velocity is nearly insensitive to our averaging procedure. The regions used for measuring density in the upstream and downstream are described in Section 3.2. The width of the reconnection layer is measured at a distance ﹩\sim 430\,c/{\omega }_{\mathrm{pe}}﹩ downstream of the central X-point. All quantities are time-averaged over ﹩\sim 0.3\,{t}_{{\rm{A}}}\approx 4500\,{\omega }_{\mathrm{pe}}^{-1}﹩. Both inflow and outflow velocities tend to decrease with ﹩{\beta }_{{\rm{i}}}﹩, with weak dependence on ﹩{T}_{{\rm{e}}}/{T}_{{\rm{i}}}﹩(noticeable only at high ﹩{\beta }_{{\rm{i}}}﹩). The density compression decreases with ﹩{\beta }_{{\rm{i}}}.﹩ The width ﹩{\delta }_{\mathrm{rec}}﹩ of the layer increases with ﹩{\beta }_{{\rm{i}}}﹩, yet with large error bars.