Image Details
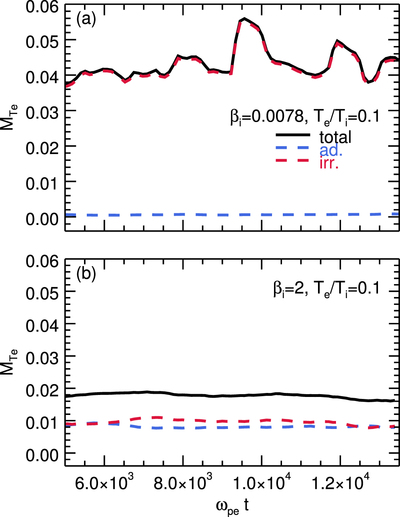
Caption: Figure 8.
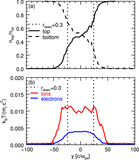
Time evolution of total (﹩{M}_{T{\rm{e}},\mathrm{tot}};﹩ black solid), irreversible (﹩{M}_{T{\rm{e}},\mathrm{irr}};﹩ red dashed), and adiabatic (﹩{M}_{T{\rm{e}},\mathrm{ad}};﹩ blue dashed) heating efficiency, for a low-﹩{\beta }_{{\rm{i}}}﹩ simulation (top panel, with ﹩{\beta }_{{\rm{i}}}=0.0078﹩) and a high-﹩{\beta }_{{\rm{i}}}﹩ case (bottom panel, with ﹩{\beta }_{{\rm{i}}}=2﹩). In both cases, ﹩{\sigma }_{w}=0.1﹩, ﹩{T}_{{\rm{e}}}/{T}_{{\rm{i}}}=0.1﹩, and ﹩{m}_{{\rm{i}}}/{m}_{{\rm{e}}}=25﹩. The heating efficiencies are measured starting at ﹩t\approx 5000\,{\omega }_{\mathrm{pe}}^{-1},﹩ at which point the two reconnection wavefronts recede past the location of the downstream region used for our computations (shown in Figure 3 with the green contours). For the low-﹩{\beta }_{{\rm{i}}}﹩ case, the total heating efficiency oscillates around ﹩{M}_{T{\rm{e}}}\approx 0.04,﹩ and it is dominated by genuine/irreversible heating (panel (a)). For high ﹩{\beta }_{{\rm{i}}},﹩ the total heating efficiency saturates at a smaller value, ﹩{M}_{T{\rm{e}}}\approx 0.016.﹩ Here, adiabatic heating and irreversible heating equally contribute (panel (b)).
Copyright and Terms & Conditions
© 2017. The American Astronomical Society. All rights reserved.