Image Details
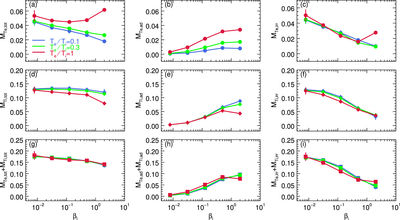
Caption: Figure 11.
For upstream temperature ratios ﹩{T}_{{\rm{e}}}/{T}_{{\rm{i}}}=0.1﹩ (blue), 0.3 (green), and 1 (red), ﹩{\beta }_{{\rm{i}}}﹩ dependence of heating efficiencies: (a) electron total, ﹩{M}_{T{\rm{e}},\mathrm{tot}};﹩ (b) electron adiabatic, ﹩{M}_{T{\rm{e}},\mathrm{ad}};﹩ (c) electron irreversible, ﹩{M}_{T{\rm{e}},\mathrm{irr}};﹩ (d) proton total, ﹩{M}_{T{\rm{i}},\mathrm{tot}};﹩ (e) proton adiabatic, ﹩{M}_{T{\rm{i}},\mathrm{ad}};﹩ (f) proton irreversible, ﹩{M}_{T{\rm{i}},\mathrm{irr}};﹩ (g) electron and proton total, ﹩{M}_{T{\rm{e}},\mathrm{tot}}+{M}_{T{\rm{i}},\mathrm{tot}};﹩ (h) electron and proton adiabatic, ﹩{M}_{T{\rm{e}},\mathrm{ad}}+{M}_{T{\rm{i}},\mathrm{ad}};﹩ (i) electron and proton irreversible, ﹩{M}_{T{\rm{e}},\mathrm{irr}}+{M}_{T{\rm{i}},\mathrm{irr}}﹩. The simulations shown here use a mass ratio ﹩{m}_{{\rm{i}}}/{m}_{{\rm{e}}}=25﹩ and magnetization ﹩{\sigma }_{w}=0.1﹩. Error bars, mostly smaller than the plotted symbols, represent one standard deviation from the mean. The decomposition of total heating into irreversible and adiabatic components shows that electron and proton heating at low ﹩{\beta }_{{\rm{i}}}﹩ is accompanied by an increase in entropy, while heating in the high-﹩{\beta }_{{\rm{i}}}﹩ regime tends to be dominated by adiabatic compression.
Copyright and Terms & Conditions
© 2017. The American Astronomical Society. All rights reserved.