Image Details

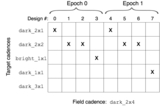
Caption: Figure 4.
Example of the definition of two different cadences, a three-epoch cadence and a two-epoch cadence, and the ways a target with the two-epoch cadence could be included in a field with this three-epoch cadence. After each epoch, the cadence defines an acceptable timing of the next epoch, as a range of days between ﹩{\delta }_{{\rm{\min }}}﹩ and ﹩{\delta }_{{\rm{\max }}}﹩; the ranges are shown as the horizontal bands for each cadence. The top row shows the three-epoch cadence; in the third epoch, we show both the range of acceptable timings relative to the first epoch (lighter band) and relative to the second epoch, assuming it was observed at the preferred timing δ. Given a target with the two-epoch cadence as shown, its timing requirements can be satisfied either by observing it in epochs 0 and 1, or epochs 1 and 2, of the three-epoch field. But its timing requirements cannot be guaranteed by observing it in epochs 0 and 2. For the two-epoch cadence to “fit” into the three-epoch cadence, the requirements on the number of observations and the sky brightness must also be satisfied. In actual operations, the roboscheduler will prefer a timing close to δ, but will not necessarily strictly respect ﹩{\delta }_{{\rm{\min }}}﹩ and ﹩{\delta }_{{\rm{\max }}}﹩.
Copyright and Terms & Conditions
© 2025. The Author(s). Published by the American Astronomical Society.