Image Details
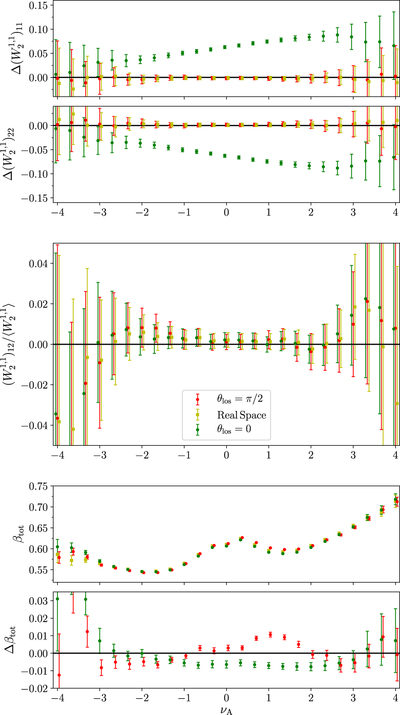
Caption: Figure 11.
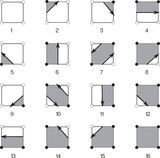
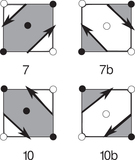
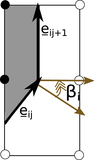
Statistics ﹩{\rm{\Delta }}{({W}_{2}^{1,1})}_{11}﹩, ﹩{\rm{\Delta }}{({W}_{2}^{1,1})}_{22}﹩, ﹩{({W}_{2}^{1,1})}_{12}/\langle {W}_{2}^{1,1}\rangle ﹩ (top and middle panels), and ﹩{\beta }_{\mathrm{tot}}﹩ (bottom panel) as a function of ﹩{\nu }_{{\rm{A}}}﹩ for the Horizon Run 4 z = 0.2 snapshot box, where we have introduced a redshift-space distortion along the line of sight. Here ﹩{\theta }_{\mathrm{los}}﹩ is the angle of the line of sight relative to the plane of the data, with ﹩{\theta }_{\mathrm{los}}=\pi /2﹩ being the usual case where the plane is perpendicular to the line of sight. The yellow squares represent the statistics in real space, and the red/green circles represent the redshift-space distorted fields perpendicular/parallel to the line of sight. The shape of individual objects ﹩{\beta }_{\mathrm{tot}}﹩ also exhibits a dependence on ﹩{\theta }_{\mathrm{los}}﹩, with excursion subsets becoming less circular in redshift space relative to the real-space field for ﹩{\theta }_{\mathrm{los}}=0﹩. In the lower right panel, we exhibit the fractional residual ﹩{\rm{\Delta }}{\beta }_{\mathrm{tot}}﹩ between ﹩{\beta }_{\mathrm{tot}}﹩ as measured in real and redshift space.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.