Image Details
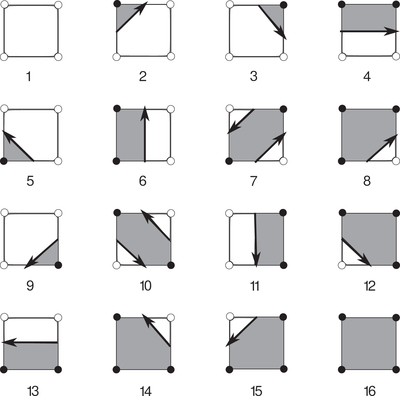
Caption: Figure 1.
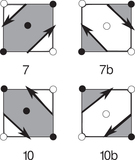
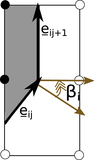
Marching-squares algorithm. Each set of four adjacent pixels for the discretized field δij can take one of 16 possible combinations of “in” or “out” states. Black circles denote points in our grid for which the density lies inside the excursion set δij > σ0ν, and white circles are “out” points with δij < σ0ν. We label each case with an integer 1 ≤ Nc ≤ 16. Between each “in” and “out” state, we linearly interpolate between corners of the box to find the point along the edge of the square that satisfies δ = σ0ν. We then connect these vertices, shown as solid black arrows. The arrow defines the boundary of the excursion region and is directed such that it always flows anticlockwise around the “in” states. The cases Nc = 7 and Nc = 10 are ambiguous, as discussed in the text.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.