Image Details
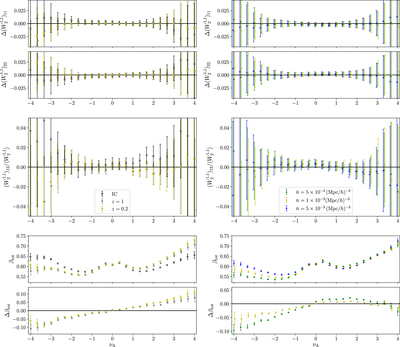
Caption: Figure 10.
Left panels: redshift evolution of the statistics ﹩{\rm{\Delta }}{({W}_{2}^{1,1})}_{11}﹩, ﹩{\rm{\Delta }}{({W}_{2}^{1,1})}_{22}﹩, ﹩{({W}_{2}^{1,1})}_{12}/\langle {W}_{2}^{1,1}\rangle ﹩ (top and middle), and ﹩{\beta }_{\mathrm{tot}}﹩ (bottom) for the Horizon Run 4 snapshot data at z = 0.2 and 1 (yellow and gray) and the Gaussian initial condition (white). We have used fiducial smoothing parameters ﹩{\rm{\Delta }}=30\,{h}^{-1}\,\mathrm{Mpc}﹩, ﹩{R}_{{\rm{G}}}=15\,{h}^{-1}\,\mathrm{Mpc}﹩. All galaxies in the simulation are used as density tracers at z = 1 and 0.2, with a total number density ﹩\bar{n}\simeq 1.5\times {10}^{-2}{({h}^{-1}\mathrm{Mpc})}^{-3}﹩. Here ﹩{\rm{\Delta }}{\beta }_{\mathrm{tot}}﹩ is the fractional difference between ﹩{\beta }_{\mathrm{tot}}﹩ as measured at ﹩z=1,0.2﹩ and the initial condition. Right panels: ﹩{\rm{\Delta }}{({W}_{2}^{1,1})}_{11}﹩, ﹩{\rm{\Delta }}{({W}_{2}^{1,1})}_{22}﹩, ﹩{({W}_{2}^{1,1})}_{12}/\langle {W}_{2}^{1,1}\rangle ﹩, and ﹩{\beta }_{\mathrm{tot}}﹩ for z = 0.2 snapshot data, taking different mass cuts to the galaxy sample to yield number density ﹩\bar{n}=5.0\times {10}^{-3}﹩, 1.0 × 10−3, and 5.0 × 10−4 (h−1 Mpc)−3 (blue, yellow, and green). Here ﹩{\rm{\Delta }}{\beta }_{\mathrm{tot}}﹩ is the fractional difference between ﹩{\beta }_{\mathrm{tot}}﹩ measured using ﹩\bar{n}=1.0\times {10}^{-3},5.0\times {10}^{-4}{({h}^{-1}\mathrm{Mpc})}^{-3}﹩ galaxy catalogs and the most dense sample ﹩\bar{n}=5.0\times {10}^{-3}{({h}^{-1}\mathrm{Mpc})}^{-3}﹩.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.