Image Details
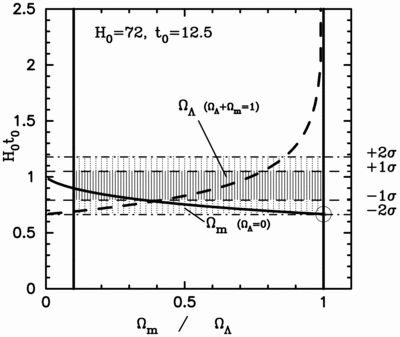
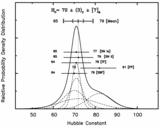
Caption: Fig. 9.
H0t0 vs. Ω for ﹩H_{0}=72﹩ km s−1 Mpc−1, ﹩t_{0}=12.5﹩ Gyr, and uncertainties of ±10% adopted for both quantities. The dark solid line indicates the case of a flat universe with ﹩\Omega _{\Lambda }+\Omega _{m}=1﹩. The abscissa in this case corresponds to ﹩\Omega _{\Lambda }﹩. The lighter curve represents a universe with ﹩\Omega _{\Lambda }=0﹩. In this case, the abscissa should be read as ﹩\Omega _{m}﹩. The dashed and dot‐dashed lines indicate 1 and 2 σ limits, respectively, for values of ﹩H_{0}=72﹩ and ﹩t_{0}=12.5﹩ Gyr in the case in which both quantities are assumed to be known to ±10% (1 σ). The large open circle denotes values of ﹩H_{0}t_{0}=\frac{2}{3}﹩ and ﹩\Omega _{m}=1﹩ (i.e., those predicted by the Einstein–de Sitter model). On the basis of a timescale comparison alone, it is not possible to discriminate between models with ﹩\Omega _{m}\sim 0.1﹩, ﹩\Omega _{\Lambda }=0﹩ or ﹩\Omega _{m}\sim 0.35﹩, ﹩\Omega _{\Lambda }\sim 0.65﹩.
Copyright and Terms & Conditions
© 2001. The American Astronomical Society. All rights reserved. Printed in U.S.A.