Image Details
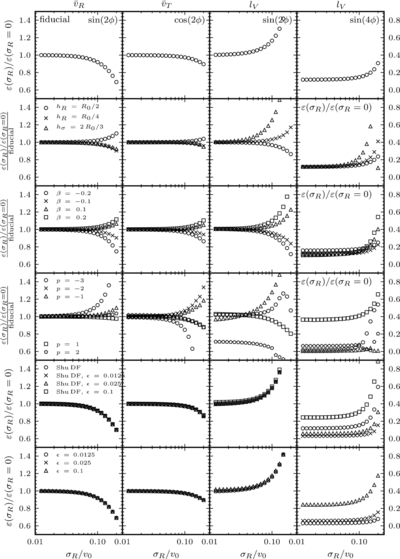
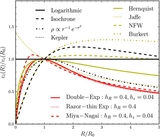
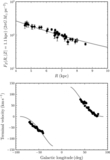
Caption: Figure 27.
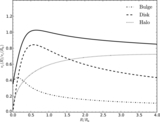
Detailed characterization of the response of a kinematically warm stellar disk to an elliptical potential perturbation. This figure displays the main non-zero Fourier components of the mean velocity and vertex-deviation response as a function of velocity dispersion σR. The response is normalized by the response of a cold disk (σR = 0; see Equations (18)–(20)). The mean radial-velocity and rotational-velocity response are well-described by a sine and cosine, respectively, of 2(ϕ − ϕb), while the vertex deviation has a substantial sin 4(ϕ − ϕb) component as well (shown in the last column; this column uses the tick marks on the right y axis). All other Fourier components are negligible (that is, they amount to less than one percent of the cold response. The top panel displays the response for the fiducial model of Figure 26: a perturbation with constant ellipticity with radius, a flat rotation curve, and an initial Dehnen DF with hR = R0/3 and hσ = R0. The lower rows demonstrate the effect of varying the parameters of this model: the second row varies the DF parameters (hR and hσ); the third row shows the effect of changing the shape of the rotation curve; the fourth row varies the radial profile of the ellipticity (which is ∝Rp). Rows two through four are normalized by the curves in the top row (except for the last column). The fifth row varies the form of the DF by showing the response for a Shu DF instead of a Dehnen DF as the initial DF; this is done for three different values of the magnitude of the perturbation. The bottom panel finally varies the magnitude of the perturbation for the Dehnen DF fiducial model. These two bottom rows demonstrate that the response is very close to linear in ![]() .
.
Copyright and Terms & Conditions
© 2015. The American Astronomical Society. All rights reserved.