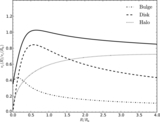
Image Details
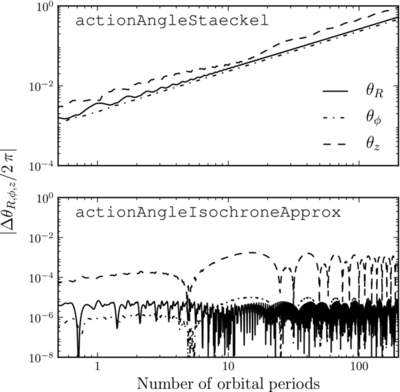
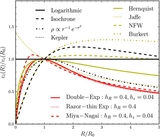
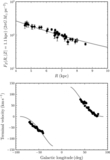
Caption: Figure 18.
Error in the angle coordinates with respect to the initial angle as a function of integration time for the same orbit and the same action–angle methods as in Figure 17 (except for actionAngleAdiabatic for which the frequencies and angles are currently not implemented). The error is computed as Δθ = θ(t) − θ(t = 0) − Ω t, where the frequency Ω is calculated as the mean frequency over the orbit. The bottom panel covers a twice-as-large range on the y axis. The errors on the radial, azimuthal, and vertical frequencies of the actionAngleStaeckel are ≈5 × 10−5, 10−3, and 2 × 10−3, respectively; for the actionAngleIsochroneApprox they are ≈4 × 10−7, 10−6, and 7 × 10−5, respectively. The smaller angle and frequency errors for actionAngleIsochroneApprox lead to angles that are stable to better than 1 in part 10−3 for hundreds of orbital periods.
Copyright and Terms & Conditions
© 2015. The American Astronomical Society. All rights reserved.