Image Details
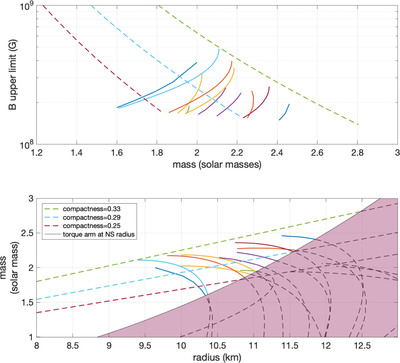
Caption: Figure 2. Magnetic field upper limits and mass–radius relations
The complete figure set (71 images) is available in the online journal.
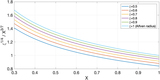
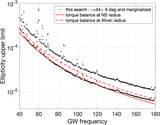
We have assumed ﹩{f}_{\mathrm{GW}}=117.5\,\mathrm{Hz}﹩ (﹩\approx 17﹩ ms spin period), ﹩\iota =44^\circ \pm 6^\circ ﹩, ﹩{r}_{m}={r}_{A}\,(\xi =1)﹩, X = 1 and torque balance. Top panel: the largest magnetic field consistent with our null result. The solid lines correspond to the equations of state from Özel & Freire (2016, http://xtreme.as.arizona.edu/NeutronStars/index.php/dense-matter-eos/). The dashed lines indicate stars of constant compactness ﹩{GM}/{{Rc}}^{2}﹩ equal to 0.33 (upper), 0.29 (middle) and 0.25 (lower). We have considered masses in the range 1 to 3 ﹩{M}_{\odot }﹩, radii between 8 and 13 km, and we have dropped any equation of state with a maximum mass lower than 1.9 ﹩{M}_{\odot }﹩, consistent with observations (Antoniadis et al. 2013; Cromartie et al. 2019) and with estimates from dense matter theory and experiment (see, for example, Hebeler et al. 2013; Kurkela et al. 2014). The lowest value of B for each curve corresponds to ﹩B({r}_{m}=R)﹩. Bottom panel: mass–radius relations for the equations of state considered above (solid lines) and for star configurations of constant compactness (dashed lines). The line that delimits the shaded region shows the mass–radius combinations that satisfy Equation (7), i.e., that are consistent with our upper limits when ﹩{r}_{m}=R﹩. Below the shaded region the torque balance gravitational-wave amplitude with ﹩{r}_{m}=R﹩, is larger than our upper limits, so these configurations are excluded by our null results. Above the shaded region the torque balance gravitational-wave amplitude with ﹩{r}_{m}=R﹩, is smaller than our upper limits, so these configurations cannot be excluded if ﹩{r}_{m}=R﹩. If, however, ﹩{r}_{m}\gt R﹩, i.e., a magnetic field above ﹩\approx 2\times {10}^{8}﹩ G, the corresponding torque balance becomes larger than our upper limits and this allows us to constrain the magnetic field (as shown in the top panel).
Copyright and Terms & Conditions
© 2021. The Author(s). Published by the American Astronomical Society.