Image Details
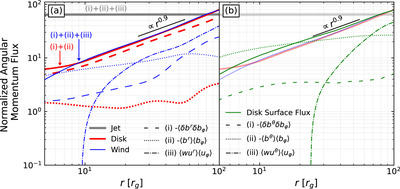
Caption: Figure 4.
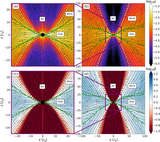
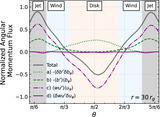
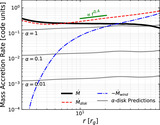
At all radii, the magnetized turbulence in the disk and laminar wind torques contribute almost equally to the radial transport of angular momentum. Here, we show the radial profile of the time- and φ-averaged decompositions of the angular momentum flux in our system. Panel (a): For each of our three main regions, we integrate ﹩{T}_{\varphi }^{r}﹩ across the θ-direction. The jet (thick solid gray line) carries a constant angular momentum outward by construction (Section 3.2). The accretion disk (thick solid red line) transports angular momentum outward with a magnitude comparable to the winds (solid blue line), and both are proportional to r 0.9. Note that we do not include the advective term (〈wu r 〉〈u φ 〉; Equation (6)) in the total disk angular momentum flux because it is negative and feeds the BH. Panel (b): The cumulative integral in radius of the angular momentum flux through the surface of the accretion disk (solid green line; see Equation (12)) has a similar magnitude as the wind and disk regions of panel (a) with the same r 0.9 dependence. For both, we further break down the angular momentum fluxes into (i) turbulent Maxwell stresses (〈δ b μ δ b φ 〉; Equation (7)) with the dashed lines, (ii) large-scale laminar Maxwell stresses (〈b μ 〉〈b φ 〉; Equation (8)) with the dotted lines, and (iii) advective transport (〈wu μ 〉〈u φ 〉; Equation (6)) with the dash–dotted lines, where μ = r, θ. The turbulent Reynolds term is negligible everywhere (see the solid purple line in Figure 3). The dashed, dotted, and dash–dotted lines sum to their respective totals described by the solid red, blue, and green lines. The angular momentum outflows within the accretion disk, in the winds, and throughout the disk surface are comparable in magnitude at all radii, and they exceed the jet-powered outflows for r > 80r g .
Copyright and Terms & Conditions
© 2024. The Author(s). Published by the American Astronomical Society.