Image Details
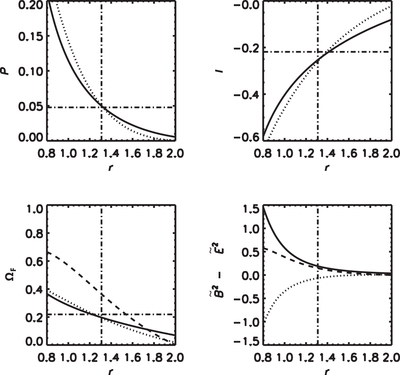
Caption: Figure 7.
FFMD simulation with the initial condition of I = 0 and ﹩{{\rm{\Omega }}}_{{\rm{F}}}=\omega -(\sqrt{{\rm{\Delta }}}/{R}^{2})\times (2M\sqrt{{\rm{\Delta }}}/{ra})﹩ at r ≤ 2M, ΩF = 0 at r > 2M as shown by the path D in Figure 6. The dashed lines show the quantities at t = 0. The dotted and solid lines show the results at t = M and t = 4 M, respectively. The horizontal dashed–dotted lines show the analytical values of the steady state, and the vertical dashed–dotted lines show the horizon of the spinning black hole. Initially, the degeneracy of the electromagnetic field is satisfied, while at t = M, it is destroyed: ﹩{\tilde{B}}^{2}-{\tilde{E}}^{2}\lt 0﹩. At t = 4 M, I and ΩF at the stretched horizon converge to the steady-state values ﹩-{B}_{0}{{\rm{\Omega }}}_{{\rm{F}}}^{\mathrm{ss}}﹩ and ﹩{{\rm{\Omega }}}_{{\rm{F}}}^{\mathrm{ss}}﹩ and the degeneracy of the field recovers. The values of P at t = M and 4M at the horizon are almost the same as the corresponding values of the analytical steady-state solution while P = 0 initially.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.