Image Details
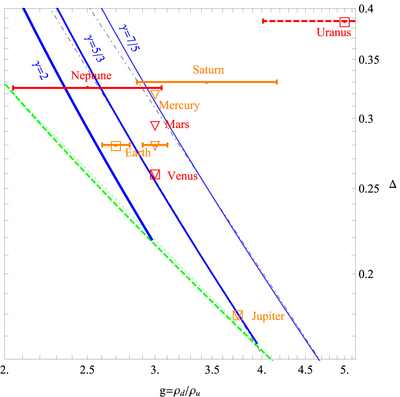
Caption: Figure 2.
Bow shock standoff distance Δ, measured from the nose of the obstacle and normalized by the nose curvature of the obstacle, plotted against the compression ratio ﹩g﹩. Analytic curves for ﹩\gamma =7/5,5/3﹩ and 2 (solid, thin to thick) are shown alongside planet data (labeled symbols), and approximated as power laws (dotted–dashed curves, see text). Also plotted is the strong shock limit for various γ (dashed), well fitted by ﹩{\rm{\Delta }}\sim 2/(3g)﹩ (dotted). Planetary g values are based on magnetic (triangle or no symbol) or density (square) compression, shown with ﹩1\sigma ﹩ error bars (when available) for Mercury (slightly perpendicular shock; measured at ﹩{\theta }_{p}\simeq 70^\circ ;﹩ Anderson et al. 2008; Treumann & Jaroschek 2008; Slavin et al. 2012), Venus (day side; Treumann & Jaroschek 2008; Frank et al. 1991), Earth (quasi-perpendicular; ﹩{\theta }_{p}\lesssim 45^\circ ;﹩ Czaykowska et al. 2000), Mars (quasi-perpendicular; ﹩{\theta }_{p}\lesssim 90^\circ ;﹩ Treumann & Jaroschek 2008), Jupiter (﹩{\theta }_{p}\simeq 20^\circ ;﹩ Gloeckler et al. 2004), Saturn (quasi-perpendicular; interval for different crossings at high angles ﹩60^\circ \lesssim {\theta }_{p}\lesssim 100^\circ ;﹩ Achilleos et al. 2006, Figure 9), Uranus (﹩{\theta }_{p}\simeq 25^\circ ;﹩ Bagenal et al. 1987), and Neptune (quasi-perpendicular; ﹩{\theta }_{p}\simeq 14^\circ ;﹩ Ness et al. 1989; Treumann & Jaroschek 2008). Standoff distances and obstacle curvatures are based on the data-constrained models of Stahara (1984, for Venus, Earth and Mars) and Spreiter & Stahara (1995, for the other planets). Systematic errors on Δ are large, especially for the external and rarely visited planets; in particular, the Δ estimate for Uranus (dashed) is inconclusive (Spreiter & Stahara 1995). For details, assumptions and limitations, see the text.
Copyright and Terms & Conditions
© 2016. The American Astronomical Society. All rights reserved.