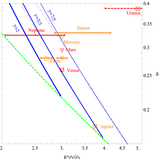
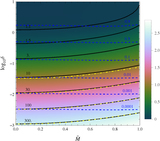
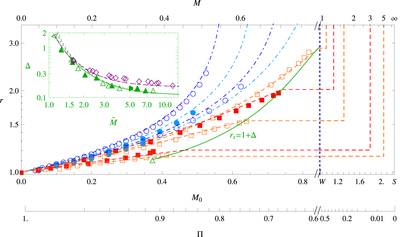
Radial profiles of Mach number M (top axis) and of normalized velocity M₀ and pressure Π (bottom axis; see definitions in Equation (4)) in front of a unit (r = 1) sphere, for ﹩\gamma =7/5﹩, according to numerical simulations (symbols) and our approximation (curves), in both subsonic (blue circles and dotted–dashed curves) and supersonic (red squares and dashed curves) regimes. Numerical data are shown (alternating shading to guide the eye) for ﹩\widetilde{M}=0.6﹩, 0.7, 0.8, 0.95 (Karanjkar 2008), 1.1, 1.3, 1.62 (Heberle et al. 1950; Krause 1975), 3 (Bono & Awruch 2008), and 5 (Sedney & Kahl 1961; Krause 1975). The shock standoff distance (solid green) with its ﹩\widetilde{M}\to \infty ﹩ limit (triangle) is also shown. The right side of the figure extends the figure (on a different scale, to show the full M range) to the supersonic, ﹩M\gt 1﹩ part of the flow, upstream of shocks; horizontal jumps represent the shock adiabat Equation (2). Inset: standoff distance measured experimentally (symbols) and using the parameter-free (dotted curves; Equation (18)) and single-parameter fit (Equation (19)) approximations, for ﹩\gamma =7/5﹩ (triangles; Heberle et al. 1950; Van Dyke 1958b; Sedney & Kahl 1961; Krause 1975; solid curve for ﹩\beta =0.48﹩) and ﹩\gamma =5/3﹩ (diamonds; Schwartz & Eckerman 1956; dashed curve for ﹩\beta =0.52﹩).