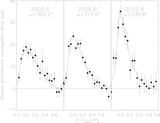
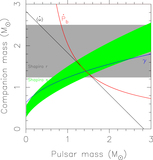
Image Details
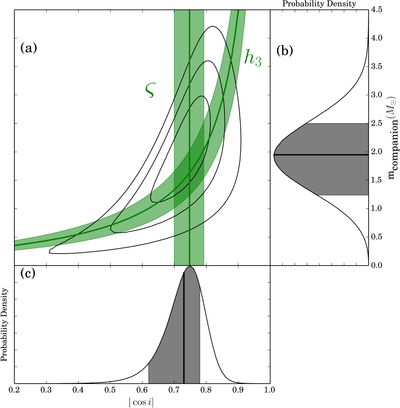
Caption: Figure 2.
(a) Measured constraints on ﹩| \cos i| ﹩ and m2 resulting from TEMPO fits for two different parametrizations of the Shapiro gravitational propagation delay within the context of general relativity. The Damour & Deruelle (1986) s and r parameters map directly onto the displayed ﹩| \cos i| \ [=+\sqrt{1-{s}^{2}}]﹩ and ﹩{m}_{2}\ [=(r/{T}_{\odot }){M}_{\odot }]﹩ axes, respectively; the black contours show joint 1, 2, and ﹩3\sigma \ ({\rm{\Delta }}{\chi }^{2}=2.3,6.2,11.8﹩) confidence limits on those quantities derived from a set of TEMPO fits to a large grid of (fixed) (﹩| \cos i| ,{m}_{2})﹩. The alternate Freire & Wex (2010) best-fit parameter constraints and their ±1σ limits are shown in green. Their fitted parameter, ς, transforms directly into the displayed ﹩| \cos i| ﹩ axis (see Equation (4)), whereas their h3 parameter does not map uniquely onto either of the axes (see Equation (5)). The marginal distributions in (b) and (c) result from collapsing the resulting two-dimensional DD probability distribution onto the ﹩| \cos i| ﹩ and m2 axes, respectively, in which the mean (solid black) and the 1σ bounds (gray region) are displayed, yielding ﹩| \cos i| =0.73\ (+0.05,-0.11)﹩ and ﹩{m}_{2}=1.95\ (+0.55,-0.71)\ {M}_{\odot }﹩ (68.3% confidence).
Copyright and Terms & Conditions
© 2016. The American Astronomical Society. All rights reserved.