Image Details
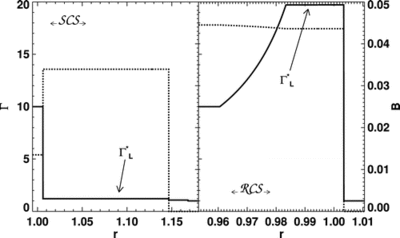
Caption: Fig. 1.
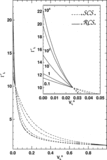
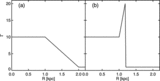
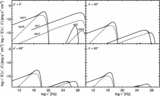
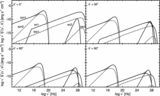
Left: Profiles of the Lorentz factor (solid line) and of the laboratory frame magnetic field (dashed line) resulting from a prototypical Riemann problem yielding a ﹩_{\leftarrow }\mathstrut{\cal S} \mathstrut{\cal C} \mathstrut{\cal S} _{\rightarrow }﹩ pattern. The initial left and right states are ﹩( p_{L},\rho _{L},v^{n}_{L},\Gamma _{L},\tilde{\beta }_{L}) =( 10^{-5},10^{-7},0.9,10,0.1) ﹩ and ﹩( p_{R},\rho _{R},v^{n}_{R},\Gamma _{R},\tilde{\beta }_{R}) =( 10^{-6},10^{-2},0,1,0.1) ﹩, respectively. Note that no boost is produced to the left of the CD located at ﹩r\simeq 1.147﹩. Right: Same as the left panel, but for a prototype ﹩_{\leftarrow }\mathstrut{\cal R} \mathstrut{\cal C} \mathstrut{\cal S} _{\rightarrow }﹩ pattern. The initial left and right states are ﹩( p_{L},\rho _{L},v^{n}_{L},\Gamma _{L},\tilde{\beta }_{L}) =( 10^{-5},10^{-7},0,10,100) ﹩ and ﹩( p_{R},\rho _{R},v^{n}_{R},\Gamma _{R},\tilde{\beta }_{R}) =( 10^{-6},10^{-2},0,1,0.1) ﹩, respectively. Note the boost (i.e., ﹩\Gamma ^{*}_{L}> \Gamma _{L}﹩) reached by the rarefied jet to the left of the CD at ﹩r\simeq 1.003﹩. In both cases, the initial discontinuity is set at ﹩r=1﹩, and the solution is shown after an arbitrary amount of time (we recall that the solution of the Riemann problem is self‐similar).
Copyright and Terms & Conditions
© 2008. The American Astronomical Society. All rights reserved. Printed in U.S.A.