Image Details
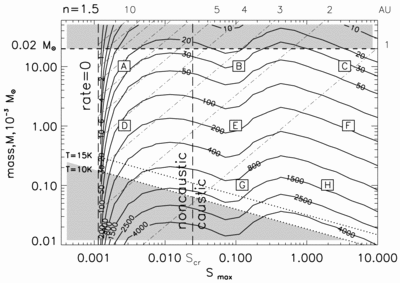
Caption: Fig. 5.
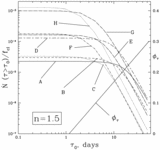
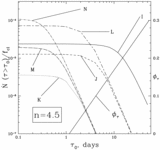
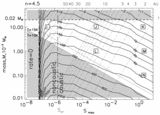
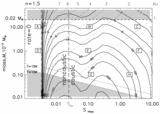
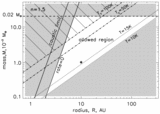
Contour plot of the rate of events with peak magnification ﹩A> A_{t}=1.1﹩ and any τ produced by gaseous lensing as function of ﹩M_{\mathrm{cl}\,}﹩ and ﹩S_{\mathrm{max}\,}\equiv 3\alpha M_{\mathrm{cl}\,}D_{\mathrm{LMC}\,}/ 16\pi R^{4}_{\mathrm{cl}\,}﹩. Each cloud is assumed to be an ﹩n=1.5﹩ polytrope. Thick solid lines represent levels of constant event rate labeled in units of ﹩10^{-6}\,\mathrm{events}\,\,\mathrm{yr}\,^{-1}﹩ per source, for ﹩f_{\mathrm{cl}\,}=1﹩. Dot‐dashed lines show the lines of constant ﹩R_{\mathrm{cl}\,}﹩ in these coordinates, labeled by ﹩R_{\mathrm{cl}\,}﹩ in AU. To the left from the thick dashed line "rate ﹩=0﹩," the clouds are unable to produce magnification ﹩A_{\mathrm{max}\,}> A_{t}=1.1﹩ (see eq. [28]). The dashed vertical line at ﹩S_{\mathrm{max}\,}=S_{\mathrm{cr}\,}﹩ separates caustic and noncaustic regimes. Dotted lines show the lower limit ﹩M_{\mathrm{cl}\,}/ R_{\mathrm{cl}\,}﹩ such that a molecule at the surface will be bound for an atmospheric temperature of 10 or 15 K. Dashed line at ﹩M=0.02﹩ M⊙ is the upper limit on ﹩M_{\mathrm{cl}\,}﹩ suggested by Wardle & Walker (1999). The unshaded region is allowed. Squares with letters show the positions of the sample cloud models from Table 1. Note the very high event rate for almost all cloud models (to the right from line "rate ﹩=0﹩").
Copyright and Terms & Conditions
© 2001. The American Astronomical Society. All rights reserved. Printed in U.S.A.