Image Details
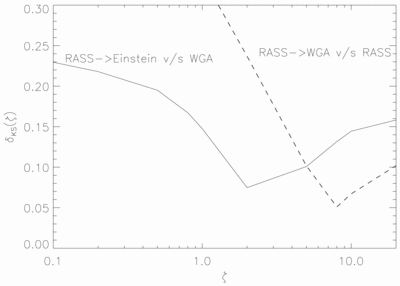
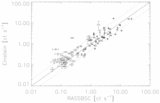
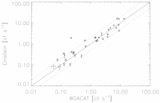
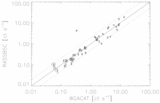
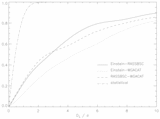
Caption: Fig. 5.
Magnitude of cyclic variability. The value of intrinsic cyclic amplitude that the selected set of stars must have in order that this variability is detectable. The maximal distance δKS(ζ) between the cumulative distributions of δ⊥ for the modeled data set and the reference data set is shown for various values of the amplitude of cyclic variability for comparisons between observations separated by "long" (solid) and "short" (dashed) time intervals. The location of the minimum indicates the best model value that fits the data. The magnitude of cyclic variability present in the long‐term (solid line) sample is ≲2. Note that the error in δKS﹩( \zeta ) \sim 0.03﹩; hence, a better estimate for the amplitude of cyclic variability is ﹩\zeta \lesssim 4﹩. In the case of the short‐term sample (dashed line), ﹩\zeta \sim 10﹩, which predicts variations that are much larger than observed over the long‐term (cf. Figs. 1–3). This latter result indicates that cycles alone cannot be responsible for the observed variability (see text).
Copyright and Terms & Conditions
© 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A.