Image Details
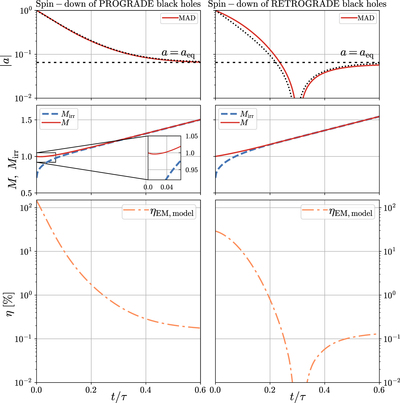
Caption: Figure 7.
Spin-down of a maximally spinning prograde BH down to the equilibrium spin results in the reduction of jet power by a factor of ∼ 103. BH spin, mass, and efficiency vs. time for prograde (left column) and retrograde (right column) MADs with initial spins of a 0 = ± 1, respectively. The time is measured in units of τ, the timescale for the BH to accrete its own mass, t/τ = m/M 0. (Top panel): BH spin exponentially decays in time, closely following the fitting formula 22. An MAD BH will spin down to a eq ≈ 0.07 by the time it has accreted a small fraction of its initial mass. For instance, a maximally spinning prograde BH spins down to a = 0.2 by t/τ = 0.2, i.e., after consuming 20% of its own mass, and to a = 0.1 by t/τ = 0.35, i.e., after consuming ≃35% of its own mass. (Middle panel): total BH mass (red solid) and irreducible BH mass (blue dashed) vs. time. At t/τ ≲ 0.04, the mass of the prograde BH briefly decreases before increasing again, as can be seen in the inset (left middle panel). This shows that BH loses rotational energy faster via the BZ mechanism than the accretion can replenish it (i.e., η > 100%). At later times, BH mass increases for both prograde and retrograde BHs. (Bottom panel): EM energy efficiency. In the prograde case, the EM efficiency drops by more than 3 orders of magnitude from a = 1 to late times, when BH spin reaches its equilibrium value, a eq ≈ 0.07. Whereas for the integration in time to obtain the a(t) dependence we use the interpolated values of s measured from the simulations, we evaluate the EM efficiency, shown in the bottom panels, using the fits given in Figure 3 and computed in Section 3.4.
Copyright and Terms & Conditions
© 2023. The Author(s). Published by the American Astronomical Society.











