Image Details
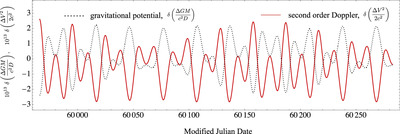
Caption: Figure 1.
The residual of the gravitational potential and second-order Doppler for MJD 59965 (2023 January 21) to MJD 60282 (2023 December 4). ΔGM = GM m − GM e and ﹩{\rm{\Delta }}{V}^{2}={V}_{m}^{2}-{V}_{e}^{2}﹩, where the subscripts refer to the Moon and the Earth, respectively, and the notation δ denotes that the quantities are residuals with the Keplerian prediction subtracted from values computed using DE440. The deviation from an ideal Keplerian orbit due to tidal dynamics causes the Moon to move faster as the separation between the Earth and the Moon decreases. The uncertainty on the estimated rate of the proper time on the Moon compared to the proper time of the Earth’s geoid depends on how the above excursions are modeled and accounted for. Without clock corrections, the inaccuracy in time and position estimates can be as high as 10% compared to clocks in well-determined orbits.
Copyright and Terms & Conditions
© 2024. The Author(s). Published by the American Astronomical Society.