Image Details
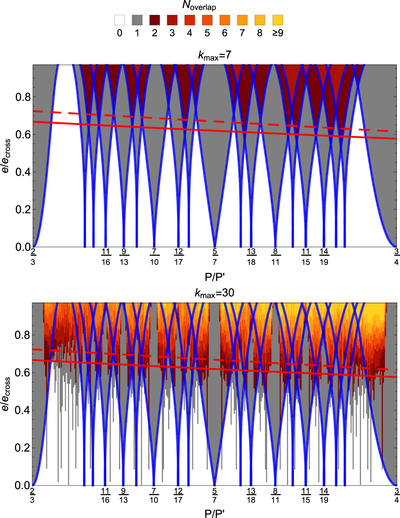
Caption: Figure 1.
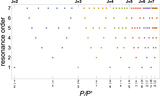
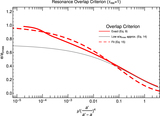
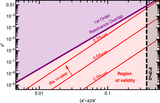
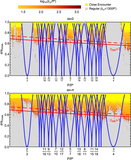
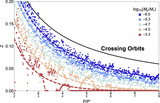
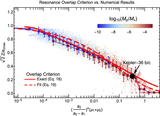
Structure of resonances and their overlap between the 3:2 and 4:3 MMRs for a test-particle perturbed by a ﹩\mu ^{\prime} ={10}^{-5}﹩ planet on a circular orbit. Blue separatrices are plotted for resonances up to seventh order. Each panel shows a grid of ﹩e/{e}_{\mathrm{cross}}﹩ vs. ﹩P/P^{\prime} ﹩, the ratio of periods of the test particle to the planet; note that ﹩{e}_{\mathrm{cross}}\approx 0.25﹩ at these periods. Grid points are colored according to the number of resonances they fall within, accounting for all resonance up to order ﹩{k}_{\max }=7﹩ in the top panel and ﹩{k}_{\max }=30﹩ in the bottom panel. Resonance widths are computed with ﹩{S}_{j,k}={s}_{k}﹩ (Equation (7)) for ﹩k\gt 7﹩ in the bottom panel. Points falling in ﹩{N}_{\mathrm{overlap}}\geqslant 2﹩ resonances are predicted to be chaotic based on the resonance overlap criterion. The solid red line marks the ﹩e/{e}_{\mathrm{cross}}﹩ value where the covering fraction of resonances is unity, i.e., ﹩{\tau }_{\mathrm{res}}=1﹩ according to Equation (10). The dashed red line marks the estimate of our fitting formula, Equation (15), for ﹩{\tau }_{\mathrm{res}}=1﹩. Note that the widths of the two k = 1 resonances at the left and right edges of the figure are represented incorrectly near e = 0 due to our adoption of the pendulum approximation. In reality, they are wider than shown at ﹩e\lesssim {(\mu ^{\prime} /j)}^{1/3}﹩, i.e., at ﹩e/{e}_{\mathrm{cross}}\lesssim 0.05﹩ in this figure.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.