Image Details
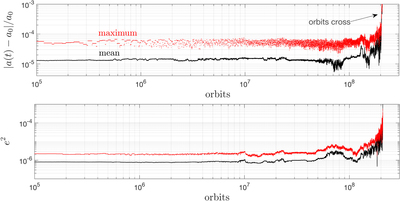
Caption: Figure 1.
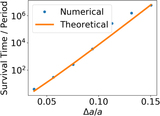
Time evolution of the relative changes in semimajor axes and eccentricity squared for the third planet in a four-planet system that becomes unstable after ∼2 × 108 orbits. These variables are proportional to the Poincaré’s actions ﹩\left|{\rm{\Lambda }}(t)-{{\rm{\Lambda }}}_{0}\right|\simeq {{\rm{\Lambda }}}_{0}| a(t)-{a}_{0}| /(2{a}_{0})﹩ and ﹩\left|{\rm{\Gamma }}(t)-{{\rm{\Gamma }}}_{0}\right|\simeq {{\rm{\Lambda }}}_{0}{e}^{2}/2﹩. The dots corresponds to the mean and maximum values using a time resolution of 100 orbits and a moving window of 104 orbits to smooth out the high-frequency oscillations. We observe that for the majority of time the action variables are bounded, until a sharp rise occurs. In contrast, if the system were to evolve by diffusion, we would expect to see a steady, power-law increase of the action variables with time. In this example, we set the mass ratio between the planets and the star to be μ = 10−7, with an equal spacing of ﹩({a}_{i+1}-{a}_{{\rm{i}}})/{a}_{1}=0.046﹩ (nearly 10 mutual Hill radii) and eccentricities to ei = 10−7, chosen such that no pair of first-order resonances overlap according to the widths calculated by Deck et al. (2012). The true anomalies and longitudes of periapse are set to {0, −1.4, 1, −1.4} and {0.9, 3.7, 3.3, 3.7} for the planets {1, 2, 3, 4}. The integration is carried out using the WHfast package (Rein & Tamayo 2015) in Rebound (Rein & Liu 2012) with ≃50 timesteps per orbit.
Copyright and Terms & Conditions
© 2020. The American Astronomical Society. All rights reserved.