Image Details
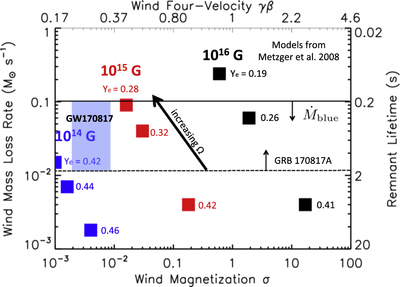
Caption: Figure 2.
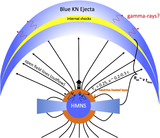
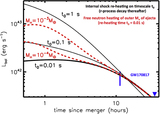
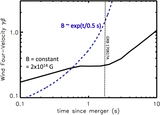
Mass-loss rate and magnetization (equivalently, asymptotic four-velocity βγ, where β = v/c, with v being wind velocity; top axis) from the steady-state, one-dimensional, neutrino-heated magnetocentrifugal wind solutions calculated by Metzger et al. (2008c). The solutions shown were calculated for a neutrino luminosity ﹩{L}_{\nu }={L}_{{\nu }_{e}}+{L}_{{\bar{\nu }}_{e}}\approx 1.4\times {10}^{52}﹩ erg s−1 and mean neutrino energies ϵνe = 11 MeV, ﹩{\epsilon }_{{\bar{\nu }}_{e}}=14﹩ MeV, similar to those from the HMNS remnant on timescales ≲1 s after the merger (Dessart et al. 2009). The right axis shows the remnant lifetime trem required to produce the total blue ejecta mass ﹩{M}_{\mathrm{blue}}\approx 2\times {10}^{-2}{M}_{\odot }﹩ of GW170817 given a constant mass-loss rate ﹩\dot{M}﹩ shown on the left axis. Each square shows a distinct steady-state solution, calculated for a different value of the surface magnetic field strength (B = 1014, 1015, 1016 G, denoted by blue, red, and black colors, respectively) and for three rotation rates (Ω = 6000, 7000, 8000 rad s−1, from bottom to top) in the range necessary for a rapidly spinning HMNS. The asymptotic electron fraction of the wind is also marked next to each solution; this value is sufficiently high Ye ≳ 0.25 to avoid significant lanthanide production for ﹩\dot{M}﹩ ≲ ﹩\dot{M}﹩blue (Equation (6); solid black line). A magnetar remnant with B ∼ (1–3) × 1014 G, Ω ≈ 9000 Hz (P ≈ 0.8 ms), and lifetime trem ≈ 0.2–2 can simultaneously explain the velocity vblue ≈ 0.3 c, total mass ﹩{M}_{\mathrm{blue}}\approx 2\times {10}^{-2}{M}_{\odot }﹩, and composition Ye ≈ 0.25–0.4 of the blue KN emission from GW170817; this concordance region is shaded in blue.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.