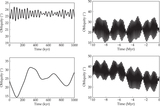
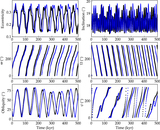
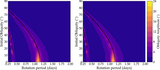
Image Details
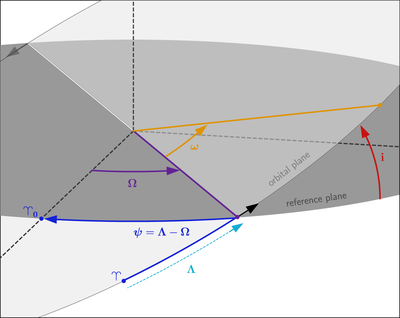
Caption: Figure 1.
Geometry used in the obliquity model DISTROT. The light gray represents the planet’s orbital plane, while the darker gray represents a plane of reference. The important orbital angles are the inclination, i, the longitude of ascending node, Ω, and the argument of pericenter, ω. The longitude of pericenter is a “dog-leg” angle, ﹩\varpi ={\rm{\Omega }}+\omega ﹩. The angle Λ is measured from the vernal point ϒ at time t to the ascending node, Ω. The precession angle is defined as ﹩\psi ={\rm{\Lambda }}-{\rm{\Omega }}﹩ (also a dog-leg angle). The reference point for Ω is usually chosen as the vernal point at some known date for the solar system, but there is probably a more sensible choice for exoplanetary systems.
Copyright and Terms & Conditions
© 2018. The American Astronomical Society. All rights reserved.