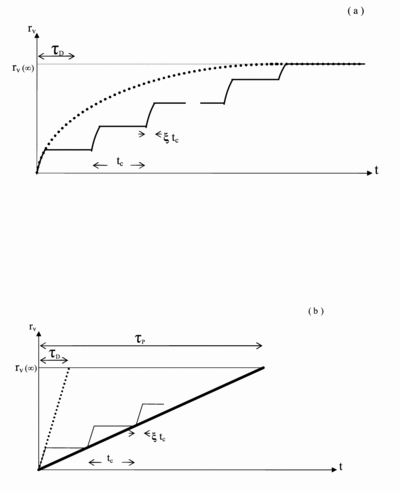
(a) Sketch of the radial displacement ﹩r_{v}﹩ of any given vortex (in a given shell) vs. time t during a rotational relaxation of the superfluid. A superfluid relaxation to an assumed final rotation frequency corresponds to a change in the vortex density, and hence to a certain radial displacement ﹩r_{v}﹩(∞) of each vortex. In the absence of any pinning (dotted line), ﹩r_{v}﹩(t) is an exponential‐like function, as in eq. (14), with an associated time constant τ_D, defined as the dynamical timescale of the superfluid. In the presence of pinning with an assumed rate ξ of random unpinning, all vortices pin and unpin intermittently with a cycle time t_c. Each vortex is described by the same function ﹩r_{v}﹩(t) as in eq. (14), however for only a time period ξt_c; then it stops and stays pinned for another time period (1 − ξ)t_c. The same cycle of motion and halt is repeated until the final displacement ﹩r_{v}﹩(∞) is reached, as required by the assumed final frequency of the superfluid in a given relaxation. (b) Same as (a), but in the linear approximation, which also makes it possible to deduce, analytically, a corresponding dynamical timescale τ_P for the pinned superfluid. The thick solid line is a convenient linear fit to the linear approximation of the actual time behavior (thin solid line) of the displacement of each vortex in the presence of pinning and random unpinning, while the dotted line is the linear approximation for the case of no pinning. Note that ξ has been greatly exaggerated, as compared with its typical expected values, for illustration.