Image Details
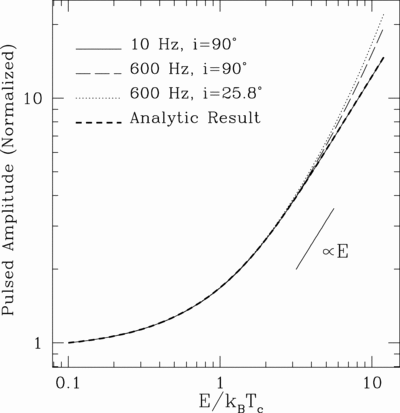
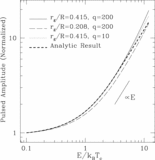
Caption: Fig. 1.
Energy dependence of the pulsed amplitude, ﹩A( E) ﹩, for both the full numerical integration and the analytic result given by eq. (10) (thick dashed line). The numerical integrations all use a ﹩q=200﹩, ﹩l=2﹩, ﹩m=1﹩ buoyant r‐mode on a ﹩M=1.4﹩ M⊙ and ﹩R=10﹩ km NS. The parameters we explore are ﹩\nu =10﹩ Hz , ﹩i=90^{\circ }﹩ (solid line); ﹩\nu =600﹩ Hz , ﹩i=90^{\circ }﹩ (long‐dashed line) and ﹩\nu =600﹩ Hz , ﹩i=25\fdg 8﹩ (dotted line). Although the normalization can change drastically for different inclinations (for an example, see Fig. 4 of Heyl 2005) we renormalize all the results to ﹩A( E) =1﹩ at ﹩E/ k_{\mathrm{B}\,}T_{c}=0.1﹩ to focus on the shape of the energy dependence. At high energies, ﹩A( E) \propto E﹩ as we show in § 2.2.
Copyright and Terms & Conditions
© 2006. The American Astronomical Society. All rights reserved. Printed in U.S.A.