Image Details
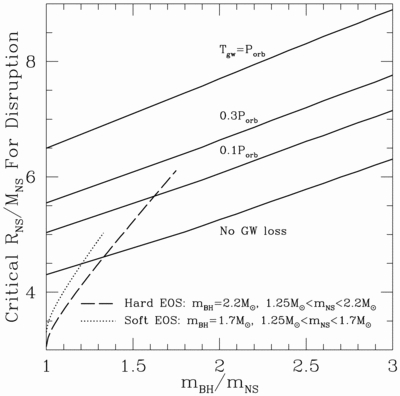
Caption: Fig. 1.
Critical radius‐to‐mass ratio for a neutron star, as a function of BH‐to‐NS mass ratio, for no rotation. Below the critical value, the neutron star is compact enough to plunge and be swallowed whole rather than be disrupted. The top solid line is constructed by assuming that the neutron star will plunge when, in one full orbit, it can reduce its angular momentum below the ISCO value via emission of gravitational radiation. The next two solid lines down reduce the allowed time to 30% and 10% of an orbit, respectively, and the bottom line ignores gravitational radiation losses entirely. For comparison, we show ﹩R_{0\,}/ m_{\mathrm{NS}\,}﹩ vs. ﹩m_{\mathrm{BH}\,\,}/ m_{\mathrm{NS}\,}﹩ for n‐body equations of state (Akmal et al. 1998) that are hard (A18+UIX+dvb, in the Akmal et al. 1998 notation; dashed line) and soft (A18; dotted line). Stars constructed with relativistic mean field theory could be somewhat larger (see Lattimer & Prakash 2001 for a recent review). In both cases we assume that ﹩m_{\mathrm{BH}\,}﹩ is just above the maximum mass of a neutron star, because this maximizes the likelihood of tidal disruption. We also consider ﹩m_{\mathrm{NS}\,}﹩ as small as ﹩1.25\,M_{\odot }﹩, which is the lowest gravitational mass yet measured for a neutron star (for PSR J0737−3039B; see Lyne et al. 2004). This figure shows that direct merger, not stable mass transfer, is the likely outcome of the coalescence of a neutron star with a nonrotating black hole.
Copyright and Terms & Conditions
© 2005. The American Astronomical Society. All rights reserved. Printed in U.S.A.



