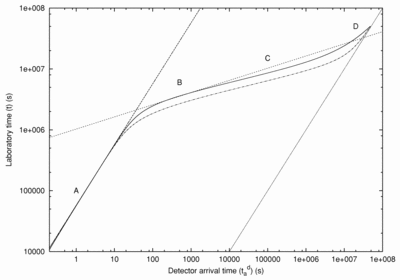
Relation between the arrival time (﹩t^{\, d}_{a}﹩) measured at the detector and the laboratory time (t) measured by an observer at rest in an inertial frame that is also at rest with the GRB source. The solid curve is computed using the exact formula given in eq. (5), incorporating as well the cosmological effects given in eq. (3), while the dash‐dotted curve is the corresponding line obtained using the approximate formula given in eq. (7), computed with the time‐varying γ given in Fig. 1. This is the approximation used by all recent works on GRBs. The difference is very conspicous, if one takes into account that the diagram is in logarithmic scale, and has basic consequences for the astrophysical scenario (see, e.g., Ruffini et al. 2001b, 2001c). We distinguish four different phases. In phase A, there is a linear relation between t and ﹩t^{\, d}_{a}﹩. In phase B, there is an "effective" power‐law relation between t and ﹩t^{\, d}_{a}﹩ (dotted line). In phase C, no single analytic formula holds; the relation between t and ﹩t^{\, d}_{a}﹩ can only be analyzed patchwise and has to be directly computed by the integration of the complete equations of energy and momentum conservation. In phase D, as the Lorentz factor approaches ﹩\gamma =1﹩, the relation between t and ﹩t^{\, d}_{a}﹩ asymptotically goes to ﹩t=t^{\, d}_{a}﹩. Details are given in Ruffini et al. (2001a).