Image Details
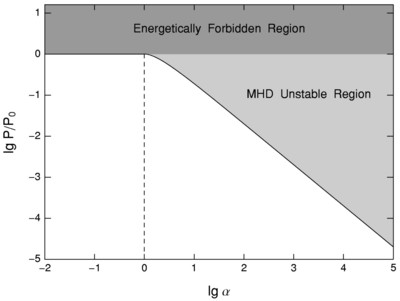
Caption: Fig. 1.
Restriction on the power P of the Blandford‐Znajek mechanism. The horizontal axis is the logarithm of ﹩\alpha \equiv La/ ( 8\pi r_{H}M) ﹩, where L is the distance from the black hole to the astrophysical loads, ﹩r_{H}﹩ is the radius of the black hole horizon, M is the mass of the black hole, and a is the angular momentum per unit mass of the black hole. The vertical axis is the logarithm of ﹩P/ P_{0}﹩, where ﹩P_{0}\equiv P( \Omega _{F}=\Omega _{H}/ 2) ﹩. The power takes its maximum at ﹩\Omega _{F}=\Omega _{H}/ 2﹩ (the impedance‐matching condition); thus ﹩P_{0}﹩ gives a universal upper bound on the power of the Blandford‐Znajek mechanism. The region with ﹩P> P_{0}﹩ is shown as thick gray region and marked "energetically forbidden region." For ﹩\alpha > 1﹩, the screw instability gives a stringent upper bound on the power. The thin gray region marked "MHD unstable region" is forbidden by the requirement that the magnetic field is stable against the screw instability. The boundary between the gray regions and the bright region is the upper bound on ﹩P/ P_{0}﹩, which is given by eq. (17) in the text. The Blandford‐Znajek mechanism can only work within the bright region. From the figure we see that the screw instability significantly restricts the power of the Blandford‐Znajek mechanism when ﹩\alpha > 1﹩. (The boundary with ﹩\alpha =1﹩ is shown as a dashed line.) For the Blandford‐Znajek mechanism to work efficiently (i.e., ﹩P/ P_{0}\approx 1﹩), we must have ﹩\alpha < 1﹩ [i.e., ﹩L< 8\pi r_{H}( M/ a) ﹩].
Copyright and Terms & Conditions
© 2000. The American Astronomical Society. All rights reserved. Printed in U.S.A.



