Image Details
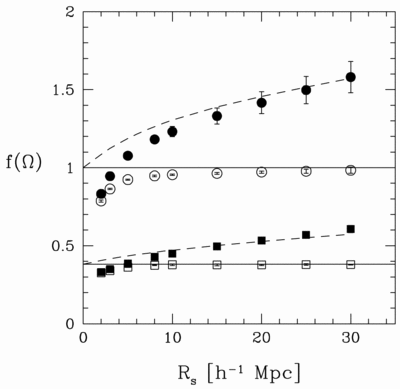
Caption: Fig. 2.
Estimates of ﹩f( \Omega _{m}) ﹩ from the slope of the relation between true galaxy velocities and velocities predicted by linear theory from the smoothed density field, as a function of the smoothing radius, ﹩R_{s}﹩, for CDM models with ﹩\Omega _{m}=1﹩ (circles) and 0.2 (squares). Points represent the mean result of four simulations of each model, and error bars show the uncertainty in the mean derived from the dispersion among the simulations. Filled symbols show the estimated ﹩f( \Omega _{m}) ﹩ when the density field is smoothed with a Gaussian filter of radius ﹩R_{s}﹩. Open symbols show the estimated ﹩f( \Omega _{m}) ﹩ when the density field is smoothed with a sharp low‐pass ﹩\boldsymbol{k}﹩‐space filter (with a cut at ﹩k_{\mathrm{cut}\,}﹩), where ﹩R_{s}﹩ is the radius of a Gaussian filter that falls to half its peak value at ﹩k=k_{\mathrm{cut}\,}﹩. Dashed lines show the linear‐theory prediction of the bias in the estimates of ﹩f( \Omega _{m}) ﹩ (eqs. [6] and [7]) from comparing smoothed velocity predictions to unsmoothed velocity measurements. Solid lines show the true values of ﹩f( \Omega _{m}) ﹩.
Copyright and Terms & Conditions
© 2000. The American Astronomical Society. All rights reserved. Printed in U.S.A.




