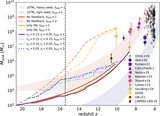
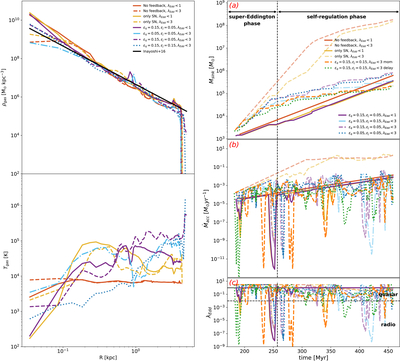
Left: the gas density and temperature profiles of our zoom-in halo at z = 10 are shown in the top and bottom panels, respectively. While the gas density profiles are broadly consistent across different simulations, which agree well with the analytical form presented in K. Inayoshi et al. (2016), the temperature profiles exhibit significant variation. This contrast highlights that, although gravitational collapse governs the overall gas distribution, the thermal state of the gas is highly sensitive to the feedback prescriptions and physical processes included in each simulation. Right: (a) The BH mass growth curves over time are shown, revealing two distinct phases. Once the BH reaches a mass of 10⁴–10⁵ M_⊙ during the super-Eddington accretion phase, AGN feedback self-regulates its growth, causing it to transition to a slower, approximately Eddington-limited rate. We refer to this stage as the self-regulation phase. (b) The evolution of the BH accretion rate (﹩{\dot{M}}_{\mathrm{acc}}﹩) over cosmic time is shown, along with (c) the Eddington ratio λ_Edd, and ﹩{\lambda }_{\mathrm{Edd}}={\dot{M}}_{\mathrm{acc}}/{\dot{M}}_{\mathrm{Edd}}﹩, which represents the accretion rate relative to the Eddington limit. During the super-Eddington phase, the BH accretion rate ﹩{\dot{M}}_{\mathrm{acc}}﹩ remains close to its maximum ﹩3\times {\dot{M}}_{\mathrm{Edd}}﹩ in the super-Eddington case and ﹩{\dot{M}}_{\mathrm{Edd}}﹩ in the Eddington-limited case. However, upon entering the self-regulation phase, only the simulations without feedback or with SN-only feedback in the super-Eddington case can sustain the maximum accretion rate. In contrast, in simulations with AGN feedback, the accretion rate inevitably declines to the Eddington limit, for the range of the implemented AGN feedback strength or the suite of SN feedback models employed.