Image Details
Caption: Figure 6.
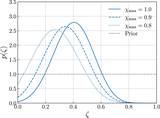
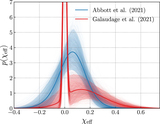
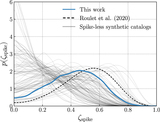
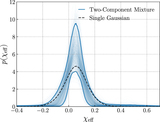
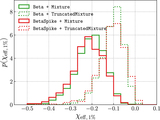
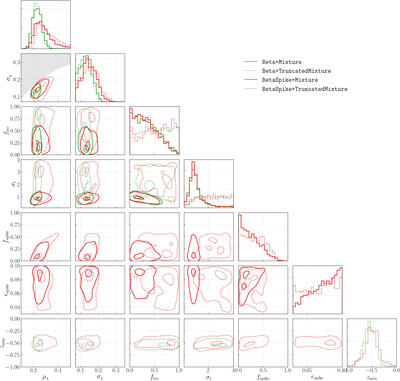
One- and two-dimensional marginalized posteriors for the parameters of each component spin model we consider (see Appendix A.2). These posteriors correspond to the measured distributions of component spin magnitudes and tilts shown above in Figure 5. Some parameters are defined only for a subset of component spin models. The shaded region in the joint μ χ –σ χ posterior is the region excluded by the prior cut on the shape parameters of the spin magnitude Beta distribution; see Appendix A.2. We find that the fraction f spike of black holes comprising a zero-spin subpopulation is consistent with zero. The data also require that at least some spins are misaligned by more than 90° relative to their Newtonian orbital angular momentum; among models that include a variable truncation bound z min on the ﹩\cos \theta ﹩ distribution, this bound is inferred to be confidently ≤ 0, regardless of assumptions about a possible zero-spin subpopulation. Allowing such a truncation bound, meanwhile, significantly impacts constraints on f iso, the fraction of binaries with isotropically oriented spins, as well as σ t , the width of a preferentially spin-aligned mixture component (see Equation (8)). As seen in Figure 5, the introduction of a truncation bound yields a significantly flatter ﹩p(\cos \theta )﹩ distribution, corresponding here to larger values of f iso and σ t .
Copyright and Terms & Conditions
© 2022. The Author(s). Published by the American Astronomical Society.