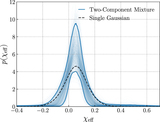
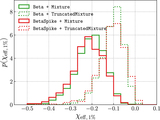
Image Details
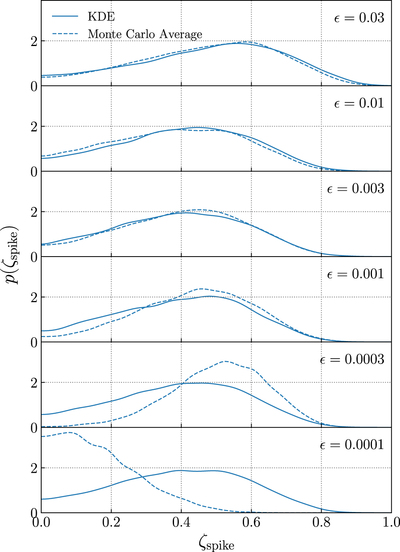
Caption: Figure 12.
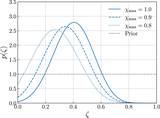
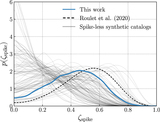
Validation of the KDE likelihood approach discussed in Appendix E. Each subplot shows the marginalized posterior for the fraction of events contained within a narrow spike at χ eff = 0. Solid lines show posteriors computed using the KDE method, while dashed lines show posteriors obtained using ordinary Monte Carlo averaging (Appendix B). Results are shown for a variety of spike widths, from broad spikes with standard deviation ϵ = 0.03 to narrow spikes with ϵ = 10−4. We see that the KDE method yields consistent and convergent results as ϵ approaches zero, while the Monte Carlo averaging gives increasingly divergent results for small spike widths due to growing Monte Carlo errors.
Copyright and Terms & Conditions
© 2022. The Author(s). Published by the American Astronomical Society.