Image Details
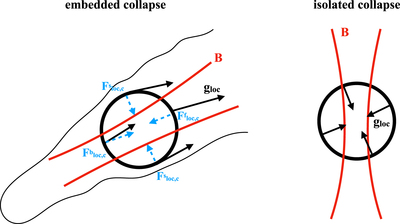
Caption: Figure 6.
Illustration of the difference between an isolated collapse (right side) and a collapse embedded in a dust lane (left side). The black circles symbolize spherical test volumes to initiate a collapse in the presence of a magnetic field (red lines). The local gravitational field, g loc, is shown with black arrows. In the case of the isolated collapse, this vector field points toward the center of the sphere, and the orientation of the magnetic field with respect to this vector field is irrelevant because g loc is azimuthally symmetric. For the embedded collapse, g loc is the result of the surrounding mass distribution. Illustrated is a typical situation as observed in Figure 3, where the local gravitational field along a filamentary dust lane is directed toward the dominating center of mass (in this case toward the right side). Generally, the individual vectors of g loc vary in length (i.e., strength of gravitational pull) and direction. The gravitational pull necessary for an embedded collapse, F loc,c, is shown with the blue dashed vectors along four symbolic directions (front, upper index “f;” back, upper index “b;” side, upper index “s”). Unlike for the isolated case, the relative orientation between field lines and g loc is pivotal because g loc is not azimuthally symmetric. As a consequence, the fraction and magnitude of g loc that is directed toward overcoming the field tension depends on this relative orientation. In particular, for the illustrated configuration, the net available gravitational pull from the sides, ﹩{F}_{\mathrm{loc},{\rm{c}}}^{{\rm{s}}}﹩, is very small if g loc and the magnetic field are prevailingly collinear.
Copyright and Terms & Conditions
© 2022. The Author(s). Published by the American Astronomical Society.