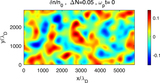
Image Details
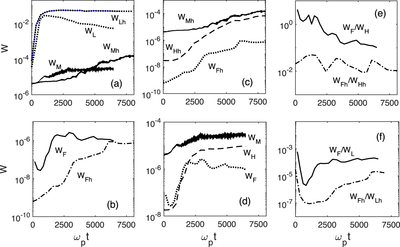
Caption: Figure 5.
Time variations of various energies W in logarithmic scales. (a) : ﹩{W}_{{ \mathcal L }h}﹩ and ﹩{W}_{{ \mathcal M }h}﹩ as well as ﹩{W}_{{ \mathcal L }}﹩ and ﹩{W}_{{ \mathcal M }};﹩ the presence (absence) of the subscript “h” refers to the case of the homogeneous plasma (inhomogeneous plasma with ΔN = 0.05); the subscripts “﹩{ \mathcal L }﹩” and “﹩{ \mathcal M }﹩” refer to the total Langmuir and the total electromagnetic energies, respectively. (b) : ﹩{W}_{{ \mathcal F }h}﹩ and ﹩{W}_{{ \mathcal F }};﹩ the subscript “﹩{ \mathcal F }﹩” refers to the electromagnetic energy at frequency ωk = ωp. (c) : ﹩{W}_{{ \mathcal M }h}﹩, ﹩{W}_{{ \mathcal H }h}﹩, and ﹩{W}_{{ \mathcal F }h}﹩ (solid, dashed, and dotted curves), for ΔN = 0; the subscript “﹩{ \mathcal H }﹩” refers to the electromagnetic energy at frequency ωk = 2ωp. (d) : ﹩{W}_{{ \mathcal M }}﹩, ﹩{W}_{{ \mathcal H }}﹩, and ﹩{W}_{{ \mathcal F }}﹩ (solid, dashed, and dotted curves), for ΔN = 0.05. (e) : ﹩{W}_{{ \mathcal F }h}/{W}_{{ \mathcal H }h}﹩ and ﹩{W}_{{ \mathcal F }}/{W}_{{ \mathcal H }}﹩. (f) : ﹩{W}_{{ \mathcal F }h}/{W}_{{ \mathcal L }h}﹩ and ﹩{W}_{{ \mathcal F }}/{W}_{{ \mathcal L }}﹩. All energies are normalized by the initial beam kinetic energy.
Copyright and Terms & Conditions
© 2022. The Author(s). Published by the American Astronomical Society.