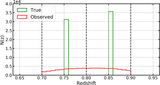
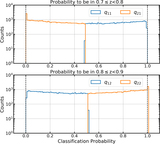
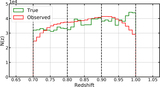
Full covariances across redshift bins for the case with three target redshift bins of Section 5.2 for an example theta bin (with θ = 0.°79 as the nominal center of the bin in log(θ)); these probe the covariances in the estimators while accounting for LSS sample variance. Here, w_αβ refers to the CF between galaxies in redshift bins α and β, and, e.g., w₁₁ and w₁₂ are correlated because LSS at the boundary of the two bins makes w₁₂ nonzero and contributes to w₁₁. As noted in the text, we calculate these full covariances as ﹩\left\langle \left\{{\widehat{w}}_{i}({\theta }_{k})-\left\langle {\widehat{w}}_{i}({\theta }_{k})\right\rangle \right\}\left\{{\widehat{w}}_{j}({\theta }_{k})-\left\langle {\widehat{w}}_{j}({\theta }_{k})\right\rangle \right\}\right\rangle ﹩ for each estimator, where i, j again run over all the correlations and the expectation value is over all the realizations. The top left panel shows the true covariances across multiple realizations of the LSS, the middle column shows covariances in contaminated samples constructed using photo-z point estimates before (top) and after (bottom) decontamination, while the rightmost column shows the covariances in CF estimates using our Weighted estimator before (top) and after (left) decontamination. We see that our new decontaminated estimators approximate the true covariances, successfully accounting for sample contamination arising from photo-z uncertainties.